
7 Hypothesis Tests and Confidence Intervals in Multiple Regression.6.5 The Distribution of the OLS Estimators in Multiple Regression.Simulation Study: Imperfect Multicollinearity.6.4 OLS Assumptions in Multiple Regression.6.3 Measures of Fit in Multiple Regression.6 Regression Models with Multiple Regressors.5.6 Using the t-Statistic in Regression When the Sample Size Is Small.Computation of Heteroskedasticity-Robust Standard Errors.Should We Care About Heteroskedasticity?.A Real-World Example for Heteroskedasticity.5.4 Heteroskedasticity and Homoskedasticity.5.3 Regression when X is a Binary Variable.5.2 Confidence Intervals for Regression Coefficients.5.1 Testing Two-Sided Hypotheses Concerning the Slope Coefficient.5 Hypothesis Tests and Confidence Intervals in the Simple Linear Regression Model.4.5 The Sampling Distribution of the OLS Estimator.Assumption 3: Large Outliers are Unlikely.Assumption 2: Independently and Identically Distributed Data.Assumption 1: The Error Term has Conditional Mean of Zero.4.2 Estimating the Coefficients of the Linear Regression Model.3.7 Scatterplots, Sample Covariance and Sample Correlation.

3.6 An Application to the Gender Gap of Earnings.3.5 Comparing Means from Different Populations.3.4 Confidence Intervals for the Population Mean.Hypothesis Testing with a Prespecified Significance Level.
LOGISTIC REGRESSION R STUDIO FULL
See our full R Tutorial Series and other blog posts regarding R programming.Ībout the Author: David Lillis has taught R to many researchers and statisticians. Lines(xanxiety, yanxiety, col= "blue", lwd = 2)Ĭlearly, those who score high on anxiety are unlikely to be admitted, possibly because their admissions test results are affected by their high level of anxiety. Plot(anxiety, success, pch = 16, xlab = "ANXIETY SCORE", ylab = "SUCCESS") Yanxiety <- predict(model_anxiety, list(anxiety=xanxiety),type="response") Clearly, the higher the score, the more likely it is that the student will be accepted. The model has produced a curve that indicates the probability that success = 1 to the numeracy score. Lines(xnumeracy, ynumeracy, col = "red", lwd = 2) Plot(numeracy, success, pch = 16, xlab = "NUMERACY SCORE", ylab = "ADMISSION") The syntax type = “response” back-transforms from a linear logit model to the original scale of the observed data (i.e. Now we use the predict() function to set up the fitted values. Ynumeracy <- predict(model_numeracy, list(numeracy=xnumeracy),type="response") A sequence from 0 to 15 is about right for plotting numeracy, while a range from 10 to 20 is good for plotting anxiety. Given the range of both numeracy and anxiety. First we set up a sequence of length values which we will use to plot the fitted model. Residual deviance: 36.374 on 48 degrees of freedom
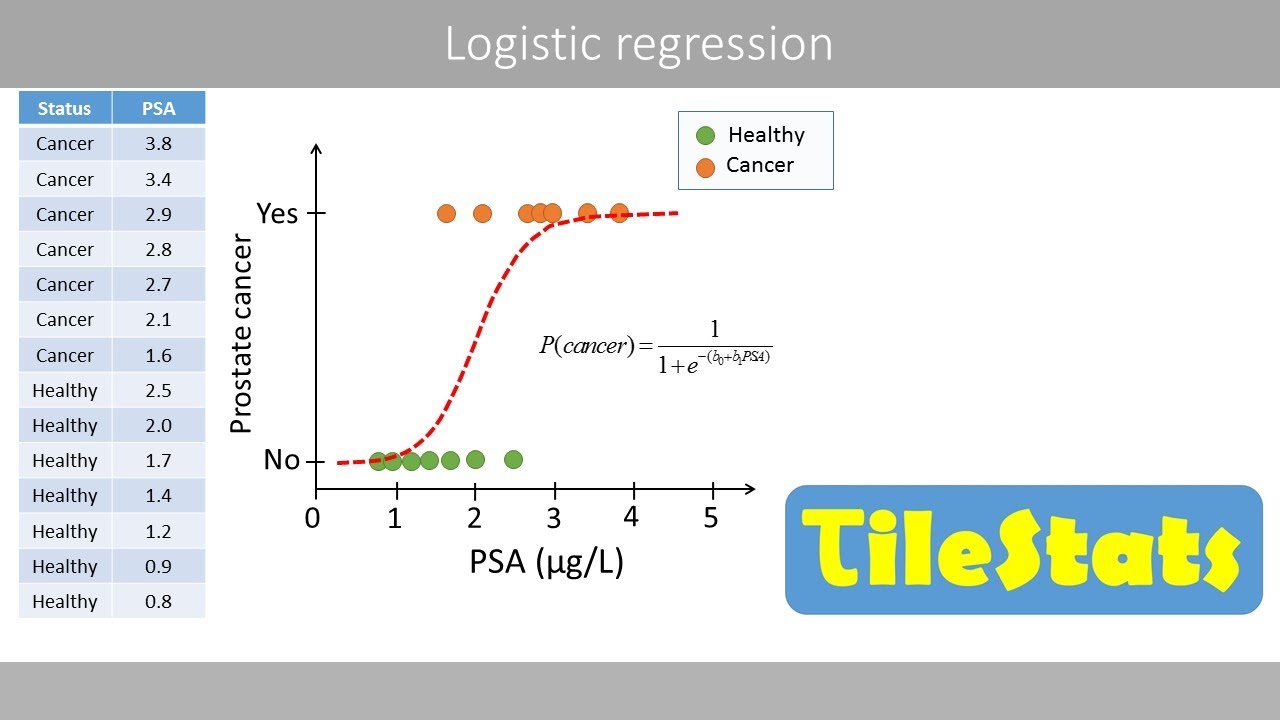
Residual deviance: 50.291 on 48 degrees of freedom Null deviance: 68.029 on 49 degrees of freedom (Dispersion parameter for binomial family taken to be 1) This isn’t the only way to do it, but one that I find especially helpful for deciding which variables should be entered as predictors. We wish to plot each predictor separately, so first we fit a separate model for each predictor. This can be very helpful for helping us understand the effect of each predictor on the probability of a 1 response on our dependent variable. Now we will create a plot for each predictor.
In my last post I used the glm() command in R to fit a logistic model with binomial errors to investigate the relationships between the numeracy and anxiety scores and their eventual success.


 0 kommentar(er)
0 kommentar(er)
